Entenda o que é e como funciona a série harmônica. Acompanhe os exemplos através da corda de um violão ou guitarra.

Natureza do próprio som

O estudo da série harmônica implica no entendimento da natureza do próprio som. Na música, a manifestação dos sons harmônicos se faz presente em áreas da teoria musical, harmonia, composição, arranjo, instrumentação e na performance de cantores e instrumentistas em geral.

Este artigo introduzirá o conceito e o princípio gerador dos primeiros harmônicos da série.

Vamos entender um pouquinho sobre este assunto?

O que é série harmônica?

Série harmônica é um fenômeno presente em qualquer som. Sua natureza se vincula ao estudo da física na área de acústica. Na perspectiva da prática musical, qualquer som emitido é constituído por outros sons que vibram junto com ele.

Desta forma, ao tocar uma nota Mi tem vários outros sons vibrando junto com o Mi. Estes sons que vibram simultaneamente e que, por vezes, não são percebidos pela escuta são chamados de “sons harmônicos”.

Já a nota principal, aquela que foi originalmente emitida é chamada de “som fundamental”. Assim, toda a série harmônica é formada a partir de um som gerador (nota fundamental) e seus sons harmônicos.

Como funciona a série harmônica?

Para demonstrar será adotado a representação da sexta corda solta de um violão ou uma guitarra, nota Mi (FIG.1) como som gerador. Ao tocar, essa corda gera uma vibração, uma onda sonora (FIG.2)

FIGURA 1 – Som gerador: nota MI, 6a corda do violão: nota MI.

FIGURA 2 – Som gerador: representação da onda sonora, ver abaixo.

Divisão da corda em partes iguais

O princípio que gera a série harmônica dessa nota Mi (som gerador) é a divisão da corda em partes iguais.

A divisão da corda em duas partes iguais (FIG.3) faz com que cada uma das partes resultantes vibre o dobro de vezes mais rápido. A resultante desta divisão será o primeiro som harmônico: a 8a do som gerador (som harmônico).

FIGURA 3 – Divisão da corda em duas partes iguais: primeiro som harmônico, a oitava do som gerador.

A representação do som gerador e seu primeiro harmônico

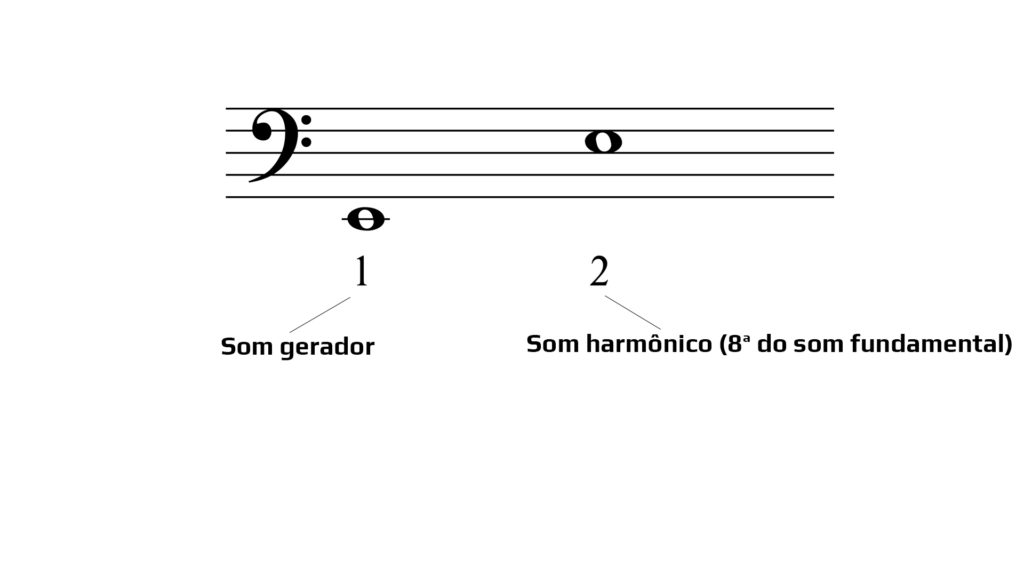
A representação do som gerador (som fundamental) é grafado como número 1 da série harmônica. O primeiro som harmônico, ou seja, a oitava do som gerador é representado pelo número 2 da série (FIG. 4).

FIGURA 4 – Representação no pentagrama do som fundamental e seu harmônico

 

 

 

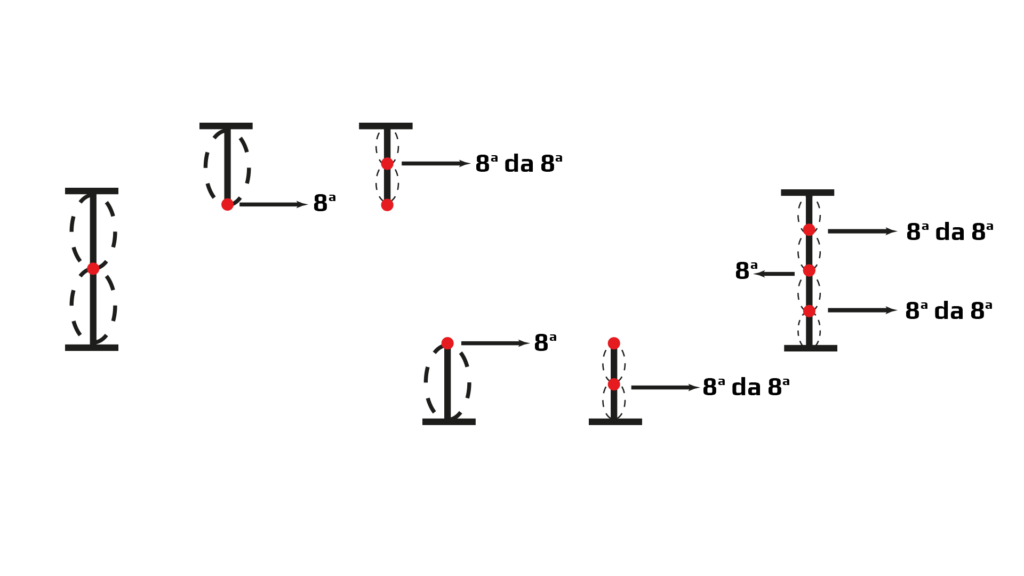
Partindo do mesmo princípio, ao dividir a corda em 4 partes iguais também resultará em oitava. Porém, será a oitava da oitava (FIG 5).

FIGURA 5 – Divisão da corda em 4 partes iguais.

Portanto, o quarto harmônico será oitava da oitava (FIG 6).

 

FIGURA 6 – Representação no pentagrama do som fundamental e seus harmônicos de oitava.

Som fundamental e todos os seus harmônicos de oitava

Para abreviar, uma forma rápida de se obter oitavas é multiplicar o som fundamental ou qualquer som harmônico por 2. Assim, todas as vezes que um som vibrar o dobro de vezes mais rápido, aparecerá a sua oitava (FIG 7). Logo, na série harmônica, todos os múltiplos de 2 serão a oitava de alguém.

FIGURA 7 – Representação no pentagrama do som fundamental e todos os seus harmônicos de oitava.

Divisão da corda em três partes iguais

Uma vez encontrados todos os harmônicos de oitava do som gerador, o próximo passo prevê a divisão da corda em três partes iguais (FIG. 8).

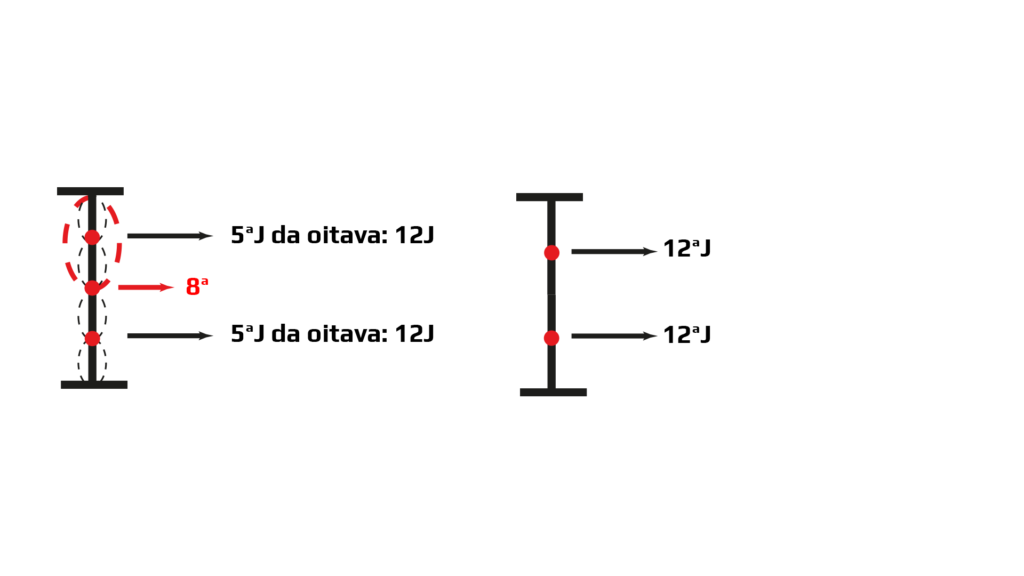
Ao realizar a divisão da corda em três, cada uma das partes será menor do que a divisão da corda em duas partes iguais (8a). Desta forma, o som resultante será mais agudo do que a oitava, uma 12aJ (5a J da oitava).

FIGURA 8 – Divisão da corda em três partes iguais: intervalo de 12aJ, ou seja, uma 5J composta.

A divisão da corda Mi em três partes iguais irá gerar a nota Si (12aJ) como som harmônico (FIG. 9).

FIGURA 9 – Representação no pentagrama do som gerador, suas oitavas e seu terceiro som harmônico (nota Si).

Aplicando o princípio de que:

a) Todas as vezes que a corda for dividida em duas partes, cada parte irá vibrar o dobro de vezes mais rápido. Harmônico resultante: 8a J.

b) Todas as vezes que a corda for dividida em três partes, cada parte irá vibrar o triplo de vezes mais rápido. Harmônico resultante: 12a J.

Representação no pentagrama dos harmônicos de oitava e quinta

Portanto, a 8aJ do terceiro harmônico ocupará o sexto lugar na série harmônica (3×2=6); a décima segunda posição na série será a oitava do sexto harmônico (6×2=12). A Figura 10 traz a representação do terceiro harmônico e suas oitavas.

FIGURA 10 – Representação no pentagrama do terceiro harmônico e suas oitavas.

Da mesma forma, a 12aJ do terceiro harmônico (nota Fá#) ocupará o nono lugar na série harmônica (3×3=9). A oitava do nono harmônico ocupará a décima oitava posição na série (9×2=18). A Figura 11 traz essa representação.

FIGURA 11 – Representação no pentagrama do terceiro harmônico e sua 12aJ.

Em resumo, qualquer som da série quando multiplicado por 2 gera sua oitava. Assim, múltiplos de 2 são oitavas de alguém.

Quando multiplicado por 3 gera sua 12aJ (5a J composta). Portanto, múltiplos de 3 são 12J de alguém.

Na continuação deste artigo será apresentada as demais divisões da corda e seus harmônicos resultantes.